After introducing non-bankable asset investing in the first article of this series, we here discuss some valuation approaches using machine learning to make nBA investing fit for total wealth management.
Read our first article of these series to get introduced to non-bankable asset (nBA) investing. Today’s piece focuses on the valuation of non-bankable assets, which we will later complement with the securitization and integration in client portfolios of nBAs to generate value for investors. Also worth noting, the next article will introduce the creation and management of a marketplace for nBA tokens to provide liquidity for investing in non-bankable assets.
The three challenges with investing in non-bankable assets
The first bridge to cross for operating non-bankable assets in a wealth management frame is to value them ex-post accurately, which is to be able to provide a reasonably accurate estimate of their price today.
To better grasp the difficulty of the task, consider the current market value of your car or, say, your (hypothetical) holiday apartment in the Swiss mountains. You may need time and research, which can be tedious, to arrive at an accurate estimate of their market value if you are ready to sell.
The second and third challenges facing the operation of non-bankable assets for investment purposes are as follows:
- how to accurately forecast the range of likely asset values over the medium to long term, which is mandatory for proper ex-ante risk analysis, and
- how to exchange nBA under the right conditions at any time. In other words, how to constantly ensure an acceptable level of liquidity for non-bankable assets at all times.
In summary, accurately estimating the current and future prices of nBAs and having a liquid market to trade them when the time comes are the minimum requirements for these alternative assets to be included in an investment portfolio alongside traditional financial assets. We will now focus on the challenge of valuing non-bankable assets.
Valuing non-bankable asset for wealth management and investing
Let us first review the fundamentals of financial asset valuation through the prism of elementary machine learning. We will then discuss extensions to deal with less standardized asset classes and focus on their most well-known representative, real estate.
One of the simplest and most accessible approaches to valuing financial security is the Capital Asset Pricing Model (CAPM), which dates back to the 1960s. This model relates the security expected return to (systematic) market risk in the simplest way, i.e. linearly as ERs = Rf + Bs(ERm - Rf), where Rf is the risk-free rate, ERs is the expected return on the security over a specified time horizon and ERm is the expected return on the so-called market portfolio over the same time horizon. Note that the market portfolio is a hypothetical portfolio made up of all the traded securities, in proportion to their presence on the market. In practice, the market portfolio is represented by an index like the SnP500 for the US stock market or the DAX index for the German market.
Despite – or because of – its simplicity, the CAPM is often not a good starting point for valuing many financial and non-bankable assets. Specifically, the theory makes strong assumptions about the market and its participants, including the assumption that information flows regularly and consistently among participants. These assumptions have been strongly challenged over the years, and some of them are now recognized as false. For example, the assumption that investors can borrow and lend at a risk-free rate, which is impossible to attain in practice. The application of the CAPM model with unverified assumptions is dangerous and has consequences unmeasurable in practice. This observation gave rise in 1976 to a more flexible and powerful valuation scheme called Arbitrage Pricing Theory (APT). In simple machine learning terms, the APT pricing formula generalizes CAPM to a multi-linear regression model. Therefore, APT also states that asset prices can be predicted from a linear relationship between expected returns on assets and a few macroeconomic variables that carry systematic risk.
The main advantage of APT over CAPM for investment is that APT allows for temporary asset mis-pricing. It is important to note that by allowing asset prices to deviate, at least temporarily, from their equilibrium value, the investor can benefit from the return of these prices to their fair value, a principle called arbitrage. Therefore, the long-term purchase of the undervalued asset and its sale at equilibrium, or conversely the short-selling of the overvalued asset and its purchase after the price has fallen, is the natural way to make a profit in this context. To do this, investors naturally need to have a good knowledge of the asset fair value or its likely supply and demand in the medium to long term. This possibility precisely differentiates investment in non-bankable assets from its traditional counterpart. Indeed, in the former case, in-depth knowledge of the asset and the market is a decisive advantage in “accurately” anticipating future movements of value. For example, the potential long-term values of a Picasso, a luxury villa in Davos or a rare Rolex or Patek Philippe can be better anticipated, from an expert's point of view, than the potential returns of liquid stocks or equity funds over a five-to-ten-year horizon (market efficiency).
From Asset Pricing to Machine Learning
The two pricing models, the APT and its particular case, the CAPM, are two simple examples of the most basic class of machine learning models, which assume linear relationships between predictors (factor returns) and the target variable (return on assets or their price). What about general situations where the linear relationship assumption does not hold, i.e. when we have good reason to believe that the predictor-target relationship is (strongly) non-linear? In this case, relying on a broken linear assumption can lead to dangerous valuation errors, which in turn can lead to a significant underestimation of the real risks associated with the assets. In any event, such a model in asset management would induce high operational and portfolio risks for the bank and the investor. Investing in a more flexible machine learning model can alleviate exposure to these risks. The following valid candidates have been used for years in wealth and portfolio management:
- Logistic regression (mainly used for classification)
- Polynomial regression (a form of linear regression where higher-order contributions of predictors are allowed, typically the variance, skewness and kurtosis of asset returns)
- Ridge and Lasso regressions (penalized linear regression models), which are commonly used to stabilize risk and return estimators and thus provide better control over costly portfolio turnover
- Non-linear regression (a generalization of polynomial regression, where a non-linear function is specified and used to model the dependency between predictors and the target value)
- Artificial neural networks (ANNs), which can capture virtually any type of dependency (specified or unspecified) between predictors and a target variable, assuming sufficient data are available to train the model. The broad category of ANN models notably includes feedforward and recurrent neural networks (RNNs), which are mainly used in the financial sector to solve complex regression and time-series prediction problems (e.g., with intraday transactions and market-making operations).
We now consider the dominant case of real estate in non-bankable asset investing and present a well-known valuation method, usually implemented as a linear or non-linear regression. We will then discuss a modern alternative based on neural networks, and mention along the way the main advantages and disadvantages of both approaches.
Hedonic pricing schemes for non-bankable assets – the real estate case
In the real estate economy, hedonic pricing models have traditionally been used to adapt to the problems of pricing products as heterogeneous as houses. In this context, they can also be used to assess the value of a property in the absence of specific data on market transactions, as well as to analyze the demand for various housing characteristics, and housing demand in general.
Hedonic models are often estimated using non-linear regression for their generality. Let us see review the ingredients and the general approach. Real-estate properties have a variety of easily measurable intrinsic characteristics, we will denote (i1,i2,...), as: year of construction, number of rooms, living area, presence of a fireplace, or a swimming pool, etc. Further, their value also depends on local and environmental characteristics (l1,l2,...), for instance: cost of living in the area and taxes, attractiveness of the location, etc. It seems obvious that building a complete hedonic model with all its data requirements – let alone maintaining them up-to-date – is no small task. It will most likely take a full-time team with a high level of expertise in real-estate appraisal to gather all the relevant data and build the right pricing model. This point applies by analogy to all non-bankable assets. Defining, using and maintaining a valuation model for non-bankable assets can be a huge task, often far removed from the core business of traditional financial intermediaries like banks, family offices, and asset/wealth managers.
So, how would the portfolio manager meet the challenge of acquiring and maintaining such capacity in-house? And, should they do so? The answer to the second question is clearly yes whenever obtaining a fair price for all assets in a portfolio is the responsibility of the portfolio manager - which is frequently the case. Furthermore, it is advisable to maintain a certain level of independence from service providers and market makers in a largely deregulated market such as the nBA one.
The remainder of the article answers the first question by focusing on real estate as the predominant instance of non-bankable assets in portfolio.
Real-estate pricing – Hedonic vs ANN
In the hedonic pricing model, the asset value is influenced by a specific mix of intrinsic and local/environmental characteristics embedded in the hedonic pricing function P.
We will write P = F(i1,i2,...,l1,l2,...), using the definitions of standard characteristics i and l in the previous paragraph. In other words, the hedonic price of a property is nothing more than a function of its intrinsic and extrinsic characteristics that influence its value. This observation shows why the hedonic valuation approach is easily generalized to other non-bankable assets such as classic cars, works of art, or virtually any valuable collectible.
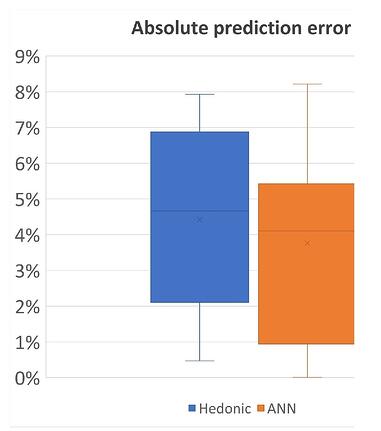
Traditionally, the estimation of P is done through the techniques mentioned in the previous paragraph, which are tried in order of complexity. First, linear and polynomial regressions and, if necessary, the use of general non-linear regressions. There is comparatively little literature on the valuation of real estate properties using neural networks (the fact that this technique is mostly unknown to real estate valuation experts is not unrelated). Nonetheless, some articles have recently been published comparing the predictive power of ANN to traditional hedonic regression for predicting the transaction price of real estate.
Figure 1 summarizes the results of one of these studies, which demonstrates the superior accuracy of ANN compared to the general hedonic regression for estimating the selling price of houses in Turkey.
In conclusion
The main advantage of ANNs over traditional hedonic regression is their flexibility. ANNs do not require some form of functional dependency to be specified between the predictors (asset characteristics) and the target (asset prices), which eliminates the risk of mis-specifying the model at that level. Instead, the network can learn the optimal price function (i.e., the one that minimizes estimation and prediction errors), provided that sufficient data on the asset and its environment are available.
Another added value of ANN compared to many econometric time series and machine learning models is that they can accommodate irregular and scattered data with no specific time-frequency. This feature, found in RNNs (e.g. LSTMs), is a great advantage for pricing non-bankable assets that are traded irregularly. These and other topical issues are dealt with in the interesting paper [2] about the valuation of real assets.
Can we conclude that neural networks and rich data sets alone are a valid substitute for field expertise when investing in non-bankable assets? No, but given advances in data processing power, they can provide financial intermediaries and investors with greater independence and insight to help them diversify their portfolios into promising alternative investment vehicles.
[1] Determinants of house prices in Turkey: Hedonic regression versus artificial neural network, Expert Systems with Applications, Vol 36, Issue 2, Part 2, March 2009, 2843-2852
[2] Machine Learning, Human Experts, and the Valuation of Real Assets, HEC Paris Research Paper No. FIN-2019-1332, 10th Miami Behavioral Finance Conference





